Cour et Exercice Corrigés mathématique tronc commun bac international-mathsbiof دروس و تمارين الرياضيات الجدع مشترك علمي بالغرنسية

Fonctions polynomiales de second degré _fonctions homographiques

I. Fonctions polynomiales de second degré :

Définition :

Soient \(\ a,b\;et\;c \) des nombres réels et non nul.On appelle fonction polynomiale de second degré toute fonction définie par : \(\ f(x )=ax²+bx+c \)

1. Les variations des fonctions : \(\ f(x )=ax²  \)

Soit \(\ f  \) une fonction numérique telle que : \(\ f(x )=ax²  \) avec \(\ a\neq 0  \) .

On a \(\ f  \) est une fonction polynomiale, donc \(\ D_f =\mathbb{R}  \) 

Alors : si  \(\ -x\in \mathbb{R} \)alors  \(\ x\in \mathbb{R} \):

Et \(\ f(-x )=a(-x)²=ax²=f(x )   \)

Par suite est une fonction paire,
Donc il suffit d’étudier la monotonie de sur l’intervalle \(\left [0 ; +\infty  \right [ \) .

Soient \(\ x_1\;et\;x_2 \) deux éléments distincts de l’intervalle \(\left [0 ; +\infty  \right [ \)  .

On a : \( T( x_1, x_2) = \frac{f(x_1 )-f(x_2 )}{x_1-x_2} = \frac{a(x_1 )²-a(x_2 )²}{x_1-x_2} \\ = \frac{a((x_1 )²-(x_2 )²)}{x_1-x_2} = \frac{a(x_1-x_2 )(x_1 +x_2) }{x_1-x_2} \\ = a(x_1+x_2)  \)

Donc :  \( T( x_1, x_2) =  a(x_1+x_2)  \)

1èr cas : si \(  a>0  \)

On a : \(\ x_1\;et\;x_2\in \left [0 ; +\infty  \right [ \)

Et on a \(  a>0  \) : donc sur \(\left [0 ; +\infty  \right [ \) :  \( T( x_1, x_2) =  a(x_1+x_2) >0  \)

Alors \(\ f  \) est une fonction strictement croissante sur  \(\left [0 ; +\infty  \right [ \)

Et puisque \(\ f  \) est une fonction paire alors est strictement décroissante sur \(\left ]-\infty  ; 0 \right ] \) .

Tableau de variations de \(\ f  \) est :

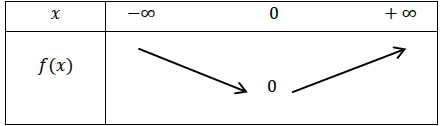
2eme cas : si \(  a>0  \)

De la même méthode, on trouve que \(\ f  \) est une fonction strictement croissante sur \(\left ]-\infty  ; 0 \right ] \) et strictement décroissante sur  \(\left [0 ; +\infty  \right [ \).

Tableau de variations de \(\ f  \) est :

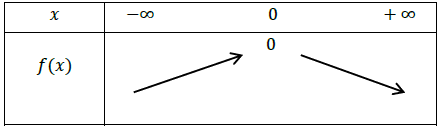
2. Représentation graphique de \(\ f:x\rightarrow ax²  \)

Définition :

Dans un repère orthonormé \( (O,I,J) \) la courbe représentative de la fonction \(\ f:x\; \rightarrow ax² \)(avec \(\  x\in \mathbb{R}^{*} \)  ) s’appelle une parabole dont les éléments caractéristiques sont son sommet qui est l’origine du repère et son axe de symétrie qui est l’axe des ordonnées. Exemple : si \( a>0 \) figire1 et si \( a<0 \) figure 2

figure1                                      figure2