Cour et Exercice Corrigés mathématique tronc commun bac international-mathsbiof دروس و تمارين الرياضيات الجدع مشترك علمي بالغرنسية

cours de la continuité pour  2BAC SVT et 2BAC PC 

binvenue dans votre site des mathematique en francais ce cour est pour les prof de lycee et pour nos elèves de 2 bac svt et 2bac pc ,cour continuité realisé par profs : Réaliser par : P.Mohamed OUTIDIR lycée el wourod kalaat megouna (un grand merci a notre prof) modifié par prof. elmoudene hassan

I. La continuité  1) La continuité en un point "Activités et cours et exemples.

Activité :

Soit f  et g  les fonctions définies sur $D_{f} et D_{g}$  par :

$$\left\{\begin{matrix} f(x)=\frac{ x^2-1 }{x-1} ; x \neq 1 \\f(1)=2& \end{matrix}\right. et \; \left\{\begin{matrix} g(x)=\frac{x^2+x}{x} ; x\neq1\\g(0)=0 \end{matrix}\right.$$

1. Calculer $\lim_{x\rightarrow 1}f(x)$ puis comparer le résultat avec $\ f(1)$ .
2. Calculer $\lim_{x\rightarrow 0}g(x)$ puis comparer le résultat avec $\ g(0)$ .
3. Que déduisez-vous ?

Définition :

Soit  une fonction numérique définie sur un intervalle ouvert $\ I$  et soit $\ x_0$  un élément de $\ I$. La fonction $\ f$  est continue en $\ x_0$ si et seulement si $\lim_{x\rightarrow x_0}f(x) = f(x_0)$  .

Exemple :

Soif  la fonction numérique définie par :  $$\left\{\begin{matrix} h(x)=x\sin x ; x \neq 0 \\h(0)=0& \end{matrix}\right.$$

Etudier la continuité de $\ h$ au point d’abscisse $\ x_0 = 0$.

Exercice d’application :

Soit  la fonction numérique suivante qui vérifie : 

$$\left\{\begin{matrix} f(x)=\frac{ \cos x -x\sin (3x) -1 }{x^2} ; x \neq 0 \\f(0)=-\frac{7}{2}& \end{matrix}\right.$$

• Etudier la continuité de $\ f$ au point d’abscisse $\ x_0 = 0$.

2. La continuité à droite $\ x_0+$  d'une fonction et sa continuité à gauche $\ x_0-$  en un point donné $\ x_0$ :

Définition :

Soit  une fonction numérique à variable réelle définie sur un intervalle du type , avec . §  On dit que  est continue à droite en $\ x_0 = 0$  si  $\lim_{x\rightarrow x_0+}f(x) = f(x_0)$ Soit  une fonction numérique à variable réelle définie sur un intervalle du type , avec . §  On dit que  est continue à gauche en $\ x_0 = 0$  si  $\lim_{x\rightarrow x_0-}f(x) = f(x_0)$. " $\ x_0+$ signifie que $x>\ x_0$ et $\ x_0-$ signifie que $x<\ x_0$ "

Exemple :

Soit $\ g$ la fonction numérique définie sur $\mathbb{R}$   par :

$$\left\{\begin{matrix} g(x)=x^2+1 \; si\; x\geqslant 1 \\ g(x)=x+ \frac{1 }{x-1} \;si\; 0<x<1 \\ g(x)=x+1 \;si\; x\leqslant0 \end{matrix}\right.$$

Etudier la continuité de la fonction $\ g$ à droite en 1 et à gauche en 0.

L’interprétation géométrique :

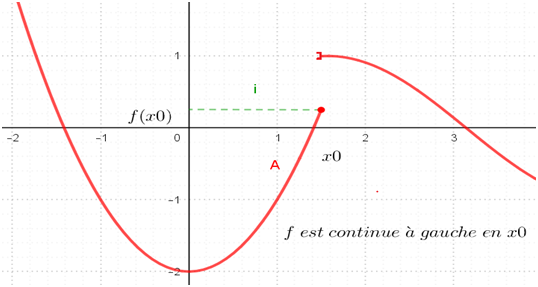
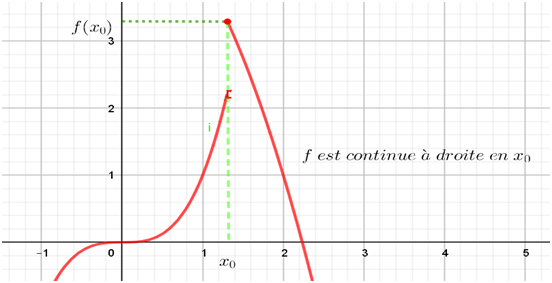
Propriété :

Soit f une fonction numérique à variable réelle définie sur un intervalle ouvert I et  $\ x_0 \in I$. La fonction  est continue en $\ x_0$ si et seulement si  est continue à droite et à gauche en $\ x_0$. c-à-d :  $\lim_{x\rightarrow x_0+}f(x) = f(x_0)$et$\lim_{x\rightarrow x_0-}f(x) = f(x_0) \Leftrightarrow lim_{x\rightarrow x_0}f(x) = f(x_0)$   .

Exercices d'applications : "sur La continuité en $\ x_0$,$\ x_0$et $\ x_0$ (trois exercices)  "

Exercice d’application 01 :

Soit $\ f$ la fonction numérique définie par :

$$\left\{\begin{matrix} f(x)=\frac{|x|}{x} ;; x\neq0 \\f(0)=-1 \end{matrix}\right.$$

1. Etudier la continuité de $\ f$ en 0.
2. Tracer la courbe de la fonction $\ f$ dans un repère orthonormé.

Exercice d’application 02:

Soit $\ f$ la fonction numérique définie par  : 

$$\left\{\begin{matrix} f(x)=\frac{ \sqrt{1+\sin x}-1}{x} ;; x<0 \\f(0)=\sqrt{1+x}-\frac{1}{2} ;; x\geqslant 0 \end{matrix}\right.$$

Etudier la continuité de la fonction $\ f$ en 0.

Exercice d’application 03:

Soient $\ a \; et \; b$ deux nombres réelles non nuls et  la fonction numérique $\ f$ définie par :

$$\left\{\begin{matrix} f(x)=ax+5b-a \;;\; x>0 \\f(0)=\frac{\sin ax}{bx} \;;\; x<0 \\f(0)=4 \end{matrix}\right.$$

• Déterminer $\ a \; et \; b$ sachant que la fonction $\ f$ est continue en $\ 0$.

3. La continuité sur un intervalle.

Définition :

La fonction $\ f$ est continue sur l’intervalle ouvert $\left ] a ; b \right [$ , si $\ f$ est continue en tout points de $\left ] a ; b \right [$ . La fonction  $\ f$ est continue sur l’intervalle $\left [ a ; b \right [$ ,si $\ f$ est continue sur l’intervalle $\left ] a ; b \right [$ et continue à droite en  $\alpha$.

Remarque :

De même, on définit la continuité de sur les intervalles du type :
$\left ] a ; b \right ] \;,\; \left [ a ; b \right ]  \;,\; \left ] a ;  +\infty  \right [\ \;,\; \left [ a ;  +\infty  \right [\;,\; \left ] -\infty  ; b \right [\;,\; \left ] -\infty  ; b \right ]\ $

Géométriquement : si $\ f$ est continue sur l’intervalle $\left [ a ; b \right ]$ , on peut tracer la courbe $\  (C)$  sans lever le crayon.

Si $\ f$ est continue sur un intervalle $\  I$ , alors $\ f$ est continue sur tout intervalle inclus dans $\  I$ .

4.    Fonction partie entière  définition + Exemple pour comprendre.

Définition :

La fonction partie entière est la fonction définie sur $\mathbb{R}$ qui à tout réel  associe l’entier relatif  tel que : $n\leqslant x< n+1$ . On note $\ E$ cette fonction.

Exemples :

$\ E(2,3)=2 \; ;\;  E(5,1)=5 \;;\; E(-7,5)=-8 \;;\; E(-17,2)=-18 \;;\; E(10)=10$

Conséquences :

Soit , on a : La fonction partie entière est continue à droite en $\ n$ et non continue à gauche en$\ n$. La fonction partie entière est continue sur l’intervalle $\left [ n ; n+1 \right [$ . La fonction partie entière est non continue en $\ n$.

......... désolé la suite et cour d’écriture .......

visité notre site demain slv  pour plus.