Cour et Exercice Corrigés mathématique tronc commun bac international-mathsbiof دروس و تمارين الرياضيات الجدع مشترك علمي بالغرنسية

Généralité sur les fonctions numériques Tronc commun biof

Activité 01 :

Considérons un rectangle de longueur (𝑥−3)𝑐𝑚 et de largeur 2𝑐𝑚 tel que 𝑥 un réel supérieur à 3.

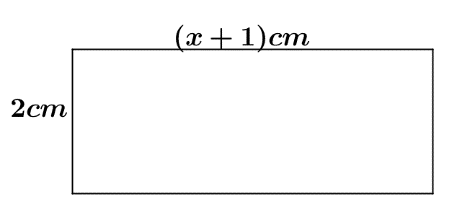
On désigne par 𝑓(𝑥) la surface de ce rectangle.

1. Déterminer l’expression de 𝑓(𝑥).
2. Déterminer la surface de ce triangle si 𝑥=4 et si 𝑥=5 .
3. Déterminer les valeurs possibles de 𝑥 si 𝑓(𝑥)=12 puis si 𝑓(𝑥)=20.

Une fonction numérique .

Définition 01 : La fonction 𝑓 est la relation qui associe tous réel 𝑥,un unique réel y. et on la note 𝑓(𝑥). On écrit alors : 𝑓(𝑥)=y .

Remarque 01 :

• L’image d’un nombre 𝑥 par la fonction 𝑓est unique et se note 𝑓(𝑥).
•  Si 𝑦 et l’image de 𝑥, on a l’égalité 𝑓(𝑥)=𝑦 et 𝑥 est appelé un antécédent de 𝑦 par la fonction 𝑓.
•  La notation suivante se rencontre également : \(𝑓:𝑥↦𝑓(𝑥)\)

Application 01 :

Soit 𝑓 une fonction définie sur l'ensemble ℝ avec : \(𝑓(𝑥)=2𝑥²−3\)

1) Déterminer les images de −2, 0 𝑒𝑡 2 par 𝑓.

2) Déterminer les antécédents, si existent, des nombres 0, 5 𝑒𝑡 −4.

Activité 02 :

Considérons 𝑓 la fonction définie par : \(𝑓(𝑥)=\frac{2𝑥}{𝑥²−1}.\)

Déterminer les images, si possible, des nombres 0, 1 𝑒𝑡 −1.

Ensemble de définition d'une fonction numérique + applications.

Définition 02 : 

 L’ensemble de définition d’une fonction 𝑓, noté souvent 𝐷𝑓, est l’ensemble des valeurs de la variable 𝑥 pour lesquelles 𝑓(𝑥) est calculable.

On écrit : 𝐷𝑓={𝑥∈𝐼𝑅/𝑓(𝑥)∈𝐼𝑅}. 

Remarque 02 :

• On dit qu’une fonction est définie sur un intervalle 𝐼 si 𝐼 est inclus dans son ensemble de définition. 

• La méthode de déterminer une ensemble de définition d’une fonction nous éliminons tous les nombre pour lesquels le dénominateur est nul et tous ce qui est sous la racine carrée doit être positif.

Application 02 :

Quelle est  l’ensemble de définition des fonctions suivantes (justifier les reponses) :

• • \(𝑓_1:𝑥↦𝑥3+12𝑥−5\)
• 
  
• • \(𝑓_2:𝑥↦\frac{−2𝑥+4}{5𝑥+3}\)
• 
  
• • \(𝑓_3:𝑥↦\frac{√𝑥}{ 2𝑥²+2𝑥−4}\)
• 
  
• • \(𝑓_4:𝑥↦\frac{4𝑥²−5}{\sqrt{2𝑥²+2𝑥−4}}\)
• 
  
• • \(𝑓_5:𝑥↦\frac{𝑥+4}{|𝑥|−3}\)
• 
  
• • \(𝑓6:𝑥↦\frac{\sqrt{2−𝑥}}{\sqrt{4𝑥+2}}\)

Fonctions égales + applications.

Définition 03 : 

Soient 𝑓 et 𝑔 deux fonctions et 𝐷𝑓 et 𝐷𝑔 ses ensembles de définition respectifs. On dit que𝑓 et 𝑔 sont égales et on écrit 𝑓=𝑔 si:

• \(𝐷_𝑓=𝐷_𝑔=𝐷\)

• \(𝑓(𝑥)=𝑔(𝑥)\) pour tout 𝑥 de \(𝐷\).

Application 03 :

Montrer que les fonctions 𝑓 et 𝑔 définies par \(𝑓(𝑥)= \frac{ \sqrt{𝑥}+2}{𝑥−4}\) et \(𝑔(𝑥)= \frac{1}{\sqrt{𝑥}−2}\) sont égales.

Considérons la fonction 𝑓 définie sur ℝ par : 𝑓(𝑥)=2𝑥+1

• 1) Remplir le tableau suivant :

𝑥	−1	2
𝑓(𝑥)

• 2) Représenter graphiquement la fonction 𝑓dans un repère orthonormé.

représentation graphiques des fonctions + applications.

Définition 04 : 

Dans un repère du plan, la courbe représentative de la fonction 𝑓, noté souvent (𝐶𝑓), est l’ensemble des points 𝑀(𝑥;𝑓(𝑥)) où 𝑥 parcourt le domaine de définition 𝐷𝑓 de la fonction 𝑓. Cette courbe a une équation s'ecrit sous la forme : 𝑦=𝑓(𝑥).

Application 04 :

Considérons 𝑓 la fonction définie par sa courbe (𝐶𝑓) représentée ci-dessous :

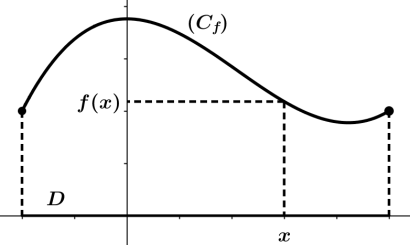
• 1) Déterminer l’ensemble de définition de 𝑓.
• 2) Remplir le tableau suivant :

𝑥	-3	-2	0	5
𝑓(𝑥)

• 3) Déterminer les antécédents par 𝑓 des nombres suivants : 0 ; −1 ; 1 et 2.

Application 05 :

Soit une fonction 𝑓 qui est définie par \(𝑓(𝑥)=\frac{𝑥²}{𝑥+1}\).

Parmi les points 𝐴(0;0),𝐵(−1;1),𝐶(3;39)𝑒𝑡 𝐷(2;4) déterminer ceux appartiennent à (𝐶𝑓). Justifier vos réponses. Soit 𝑓 une fonction et (𝐶𝑓) sa courbe dans un repère du plan. • Pour déterminer les points d’intersection de (𝐶𝑓) avec l’axe des abscisses, on résoudre l’équation 𝑓(𝑥)=0 tel que 𝑥∈𝐷𝑓. • Si 0∈𝐷𝑓, alors le point d’intersection de (𝐶𝑓) avec l’axe des ordonnées est : 𝐴(0,𝑓(0))

Application 06 :

Considérons 𝑓la fonction définie par : 𝑓(𝑥)=𝑥²+2𝑥−8.

Déterminer les points d’intersection de \((𝐶_𝑓)\) avec les axes du repère

Activité 04 :

Soient f la fonction définie par sa courbe \((𝐶_f)\) représentée ci-dessous :

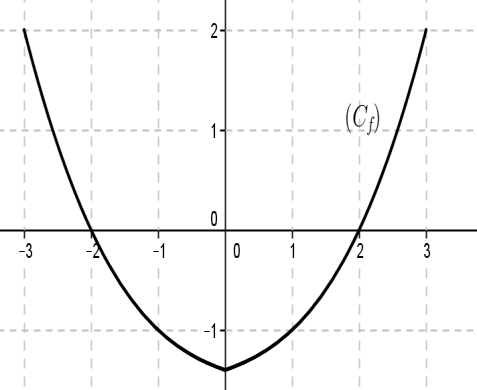
1.  Déterminer l’ensemble de définition de 𝑓.
2. Comparer 𝑓(−2) 𝑒𝑡 𝑓(2) puis 𝑓(−3) 𝑒𝑡 𝑓(3).
3. Soit 𝑥∈𝐷𝑓, comparer 𝑓(−𝑥) 𝑒𝑡 𝑓(𝑥).
4. Quelle est la propriété géométrique vérifiée par (𝐶𝑓) ? 

Fonction Paire et ces propriétés + applications simples .

Définition 05 : 

Soit 𝑓 une fonction numérique définie sur 𝐷𝑓. On dit que 𝑓 est paire si les deux conditions suivantes sont vérifiées : 

1. −𝑥∈𝐷𝑓 pour tout 𝑥 de 𝐷𝑓. 
2. 𝑓(−𝑥)=𝑓(𝑥) pour tout 𝑥 de 𝐷𝑓. 

Remarque 04 :

la courbe de 𝑓est symétrique par rapport à l’axe des ordonnées si et seulement si 𝑓 est paire.

Activité 05 :

Soit 𝑓 une fonction définie par la courbe \((𝐶_𝑓)\) représentée ci-dessous :

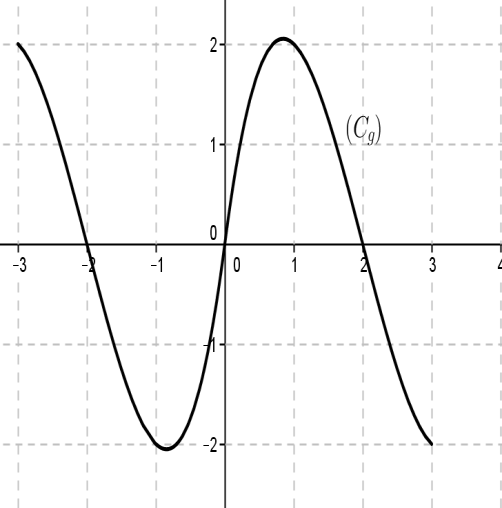
1.  Déterminer l’ensemble de définition de 𝑓.
2. Comparer 𝑓(−3) 𝑒𝑡 𝑓(3) puis 𝑓(−1) 𝑒𝑡 𝑓(1).
3.  Soit 𝑥∈𝐷𝑓, comparer 𝑓(−𝑥) 𝑒𝑡 𝑓(𝑥).
4. Quelle est la propriété géométrique vérifiée par \((𝐶_𝑓)\) ? 

Fonctions impaires et leurs propriétés .

Définition 06 :

Soit 𝑓 une fonction numérique définie sur 𝐷𝑓. On dit que 𝑓 est impaire si les deux conditions suivantes sont vérifiées : • −𝑥∈𝐷𝑓 pour tout 𝑥 de 𝐷𝑓. • 𝑓(−𝑥)=−𝑓(𝑥) pour tout 𝑥 de 𝐷𝑓.

Remarque 05 :

𝑓 est impaire si et seulement si sa courbe est symétrique par rapport à l’origine du repère.

Application 07 :

Etudier la parité des fonctions suivantes :

• \(𝑓_1:𝑥↦|𝑥|−\frac{1}{𝑥²}\)

• \(𝑓_2:𝑥↦\frac{𝑥}{𝑥²−1}\)

• \(𝑓_3:𝑥↦\sqrt{𝑥}+1\)

• \(𝑓_4:𝑥↦𝑥²+𝑥−3\)

•\(𝑓_5:𝑥↦|𝑥−1|−|𝑥+1|\)

Application 08 : 

Soient 𝑓et 𝑔 des fonctions Sont ensemble de définition est : [−5;5] et ses courbes respectives \((𝐶_𝑓)\) et \((𝐶_𝑔)\) représentées ci-dessous :

Compléter(𝐶𝑓) sachant que 𝑓est paire et \((𝐶_𝑔)\) sachant que 𝑔est impaire.

Activité 06:

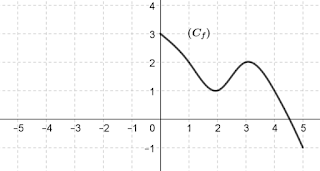
Considérons 𝑓 la fonction définie par sa courbe représentée ci-dessous :

1) Déterminer \(𝐷_𝑓\).

2) Soient 𝑎 et 𝑏 deux nombres de [−3;−1] tels que 𝑎<𝑏.

Comparer graphiquement 𝑓(𝑎) et 𝑓(𝑏).

3) Soient 𝑎 et 𝑏 deux nombres de [−1;2] tels que 𝑎<𝑏.

Comparer graphiquement 𝑓(𝑎) et 𝑓(𝑏).

4) Compléter le tableau suivant :

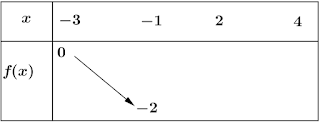
5) Déterminer la valeur maximale et la valeur minimale de 𝑓 sur [−3;4]. 

La Monotonie des + des applications simples .

Définition 07 : 

Soient 𝑓 une fonction et 𝐼 un intervalle inclus dans son ensemble de définition . • 𝑓 est (resp. ) sur 𝐼 si pour tous réels 𝑎 et 𝑏 appartenant à 𝐼 tels que 𝑎<𝑏 , on a : 𝑓(𝑎)<𝑓(𝑏) (resp. 𝑓(𝑎)≤𝑓(𝑏) ). • 𝑓 est (resp. ) sur 𝐼 si pour tous réels 𝑎 et 𝑏 appartenant à 𝐼 tels que 𝑎<𝑏 , on a : 𝑓(𝑎)>𝑓(𝑏) (resp. 𝑓(𝑎)≥𝑓(𝑏)). • 𝑓 est sur 𝐼 si pour tous réels 𝑎 et 𝑏 appartenant à 𝐼 tels que 𝑎<𝑏 , on a : 𝑓(𝑎)=𝑓(𝑏). • 𝑓 est (resp. ) sur 𝐼 s’elle est strictement croissante (resp. Croissante) ou strictement décroissante (resp. Décroissante) sur 𝐼.

Application 09 :

Considérons 𝑓 la fonction définie sur 𝐼𝑅 par : 𝑓(𝑥)=2𝑥²+3.

• 1) Soient 𝑎 et 𝑏 deux éléments de l’intervalle [0;+∞[ tels que : 𝑎<𝑏 .
• a)-Montrer que : 𝑓(𝑎)<𝑓(𝑏) .
• b)-En déduire la monotonie de𝑓 sur [0;+∞[ .
• 2) Etudier la monotonie de𝑓 sur]−∞,0] .
• 3) Dresser le tableau de variations de 𝑓.

Application 10 :

Dresser le tableau des variations de la fonction 𝑓 représentée par sa courbe ci-dessous :

Taux de variation d'une fonction numérique + Applications .

Définition 08 : 

Soient 𝑓 une fonction numérique et 𝐷𝑓 son ensemble de définition et soient 𝑎 et 𝑏 deux nombres distincts de 𝐷𝑓 . Le nombre réel 𝑇=𝑓(𝑏)−𝑓(𝑎)𝑏−𝑎est appelé taux de variation de 𝑓 entre 𝑎 et 𝑏 .

Propriété 01 :

 Soient 𝑓 une fonction numérique et 𝑇son taux de variation entre deux nombres distincts 𝑎 et 𝑏 d’un intervalle𝐼 inclus dans son ensemble de définition . 

• Si 𝑇>0 (resp. 𝑇≥0) pour tous 𝑎 et 𝑏 de 𝐼, alors𝑓est strictement croissante (resp. Croissante) sur 𝐼 .
• Si 𝑇<0 (resp. 𝑇≤0) pour tous 𝑎et 𝑏de 𝐼, alors 𝑓est strictement décroissante (resp. Décroissante) sur 𝐼 
• Si 𝑇=0 pour tous 𝑎et 𝑏 de 𝐼 , alors 𝑓 est constante sur 𝐼.

Application 11 :

Considérons la fonction définie par : 𝑓(𝑥)=𝑥²−6𝑥+5

1. Montrer que le taux de variation de 𝑓 entre deux nombres distincts 𝑎 et 𝑏 est : 𝑇=𝑎+𝑏−6 .
2. Etudier la monotonie de𝑓 sur chacun des intervalles ]−∞;3] et [3;+∞[.
3. Dresser le tableau de variations de 𝑓. 

Extremum Valeurs minimale et valeur maximal + Application

Définition 09 : 

Soient 𝑓 une fonction numérique et 𝐷𝑓son ensemble de définition et 𝐼un intervalle inclus dans\(𝐷_𝑓\) et 𝑎 un réel de 𝐼 . 

• • On dit que 𝑓(𝑎) est le minimum (ou la valeur minimale) de 𝑓 sur 𝐼 si pour tout 𝑥 de 𝐼 on a : 𝑓(𝑥) ≥ 𝑓(𝑎). 
• • On dit que 𝑓(𝑎) est le maximum (ou la valeur maximale) de𝑓 sur 𝐼 si pour tout 𝑥 de 𝐼 on a : 𝑓(𝑥) ≤ 𝑓(𝑎) . 
• • On dit que 𝑓(𝑎) est un extremum de𝑓 sur 𝐼 si𝑓(𝑎) est la valeur maximale ou la valeur minimale de 𝑓 sur 𝐼 .

Application 12 :

Soit 𝑓une fonction numérique définie sur 𝐼𝑅 par :  𝑓(𝑥)=𝑥²−2𝑥+5.

1. Calculer 𝑓(1).
2. Montrer que :𝑓(𝑥) ≥ 4 Pour tout 𝑥 ∈ 𝐼𝑅.
3.  qu’est ce que vous déduisez ? 

Propriété 01 :

Soient 𝑓 𝑒𝑡 𝑔 deux fonctions et 𝐷 un ensemble inclus dans \(𝐷_𝑓∩𝐷_𝑔\). 

• Dire que pour tout 𝑥∈𝐷 : 𝑓( 𝑥 )>𝑔 ( 𝑥) revient à dire que (𝐶𝑓) est strictement au-dessus de (𝐶𝑔) sur 𝐷. 
• Dire que pour tout 𝑥∈𝐷 : 𝑓( 𝑥 )≤𝑔 ( 𝑥) revient à dire que (𝐶𝑓) est au-dessous de (𝐶𝑔) sur 𝐷. 
• Dire que 𝑓( 𝑎 )= 𝑔 ( 𝑎) (avec 𝑎 ∈ 𝐷) revient à dire que (𝐶𝑓) et (𝐶𝑔) se coupe au point d’abscisse 𝑎

Application 13 :

Les fonctions 𝑓 et 𝑔 sont définies sur 𝐼𝑅 ; leurs représentations graphiques sont données ci-dessous

1. Résoudre graphiquement l’équation 𝑓(𝑥) = 𝑔(𝑥).
2.  Résoudre graphiquement les inéquations suivantes :

•  𝑓(𝑥) ≤ 𝑔(𝑥) .
• 𝑓(𝑥) > 𝑔(𝑥) .

Propriété 03 :

Soient 𝑓 une fonction et \(𝐷⊂𝐷_𝑓\) et 𝑘 un nombre réel. 

• • Dire que pour tout 𝑥∈𝐷 : 𝑓( 𝑥 ) > 𝑘 revient à dire que (𝐶𝑓) est strictement au-dessus de la droite d’équation : 𝑦=𝑘 sur 𝐷. 
• • Dire que pour tout 𝑥∈𝐷 : 𝑓( 𝑥 ) ≤ 𝑘 revient à dire que \((𝐶_𝑓)\) est au-dessous de de la droite d’équation : 𝑦=𝑘 sur 𝐷.

Application 14 :

Soit une fonction 𝑓 qui est définie par sa courbe représentée ci-dessous :

1. 1) Donner l’ensemble de définition de 𝑓.
2. 2) Résoudre graphiquement les équations 𝑓(𝑥)=0 et 𝑓(𝑥)=−1.
3. 3) Résoudre graphiquement les inéquations suivantes :

Exercices sur les fonction numériques :

Exercice 01 :

Soit 𝑓 la fonction représentée par courbe ci-dessous :

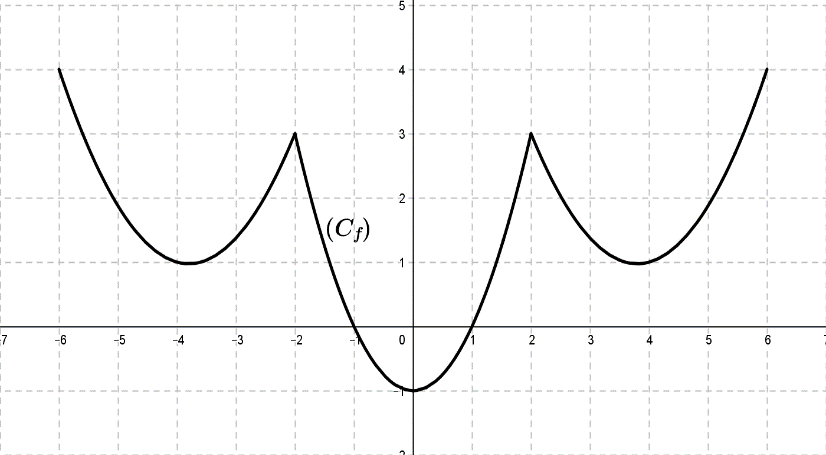
1. Donner 𝐷𝑓 .
2. Déterminer la parité de la fonction 𝑓.
3. Donner le tableau de variations de 𝑓.
4. Déterminer la valeur maximale el la valeur minimale de 𝑓 sur 𝐷𝑓 puis sur [1;5].
5. Résoudre graphiquement les inéquations suivantes :

• • 𝑓(𝑥)<0 .
• • 𝑓(𝑥)≥0 .

ce cour est réalisé par prof : latrach abdelkabir (un grand merci a notre prof )